
亨利·庞加莱(1854–1912)曾说:“我们依靠逻辑去证明,却靠直觉去发现。”
在任何形式化的思想体系中,总会有一些预设前提——也就是被视为根本正确的事实。在数学中,学生们有时被要求接受一些看起来毫无道理的事实,仅仅是为了逻辑上的一致性。例如皮亚诺公理、欧几里得的平行公设,或者选择公理。

在这篇文章中,我们来探讨一个有趣的事实,它出现在阶乘函数的语境中。阶乘函数用感叹号“!”表示,它的定义是将一个正整数 n 与它以下的所有正整数相乘:
n! = n × (n − 1) × (n − 2) × (n − 3) × … × 1
比如:
5! = 5 × 4 × 3 × 2 × 1 = 120
那么,当我们遇到 0! 的时候,会发生什么呢?我们将从最不直观的角度出发,逐步建立起对这一数学“事实”的深刻直觉理解。
空乘积约定
所谓“空乘积”约定,是一个典型的保持一致性的数学规则。阶乘本质上是一种连乘。在数学中,每当我们谈到一系列因子的乘积时(比如一堆数相乘),我们通常的意思是这样的:
a₁ × a₂ × a₃ × … × aₙ
那么问题来了:如果一个因子也没有,那我们还谈什么乘积呢?空乘积约定告诉我们:当乘积中没有任何因子时,其值被定义为 1。
这和加法中的“空加和”很类似——当一组数为空时,加法的结果被定义为 0,因为 0 是加法的单位元。同样地,在乘法中,1 是乘法的单位元,所以“没有任何数相乘”的结果就定义为 1,听起来也算合理。
打个比方,假设我们拿数字 27 来举例。它可以拆成 3 × 3 × 3,一共三个因子。我们每次除以 3,相当于去掉一个因子:第一次除后剩下 3 × 3,再除一次剩下 3,最后再除一次,就没有因子了,只剩下乘法单位元 1。从这个角度来看,完全清除所有因子得到的结果是 1,这便很好地解释了为何:
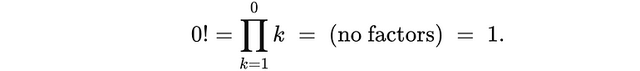
递归法
理解 0! = 1 最清晰的方式之一,是通过观察阶乘函数随 n 减小时的规律。假设我们从 n = 4 开始:
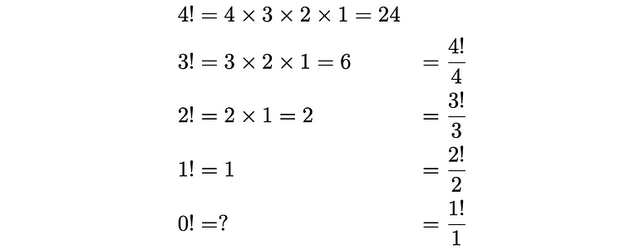
注意,这里我们可以看出一种规律性的关系:
n! = n × (n − 1)!
这是阶乘函数的递归定义。
根据这个定义,当 n = 1 时:
1! = 1 × 0!
我们知道 1! = 1,因此:
这个推导过程没有任何漏洞,全然是逻辑的演绎。换言之,如果我们希望阶乘函数在所有整数 n ≥ 0 上保持一致的递归结构,那么我们必须定义 0! = 1,否则公式 n! = n × (n − 1)! 就在 n = 1 的时候崩溃了。
计数论解释
我个人最喜欢的视角是从“如何计数”来理解这个问题。这里有两个密切相关的概念:排列和组合。
排列指的是对 n 个不同对象进行有序排列的方式数。举个例子:
有 3 个乐高小人:艾玛(Emma)、奥莉(Ollie)和艾莉娅(Aliya),那么可以有几种不同的排列方式?
答案是:3! = 6 种
现在我们把奥莉移除,只剩下艾玛和艾莉娅,那么排列方式是:
2! = 2 种
再移除艾莉娅,只剩下艾玛一个人,此时排列方式为:
1! = 1 种
最后,我们把艾玛也移除。请问:0 个对象可以有几种排列方式?
答案是:只有一种。
换句话说,空集 { } 只有一种排列方式——那就是“什么也不排”,也就是空排列本身。这就是:
0! = 1
换个角度,从组合的角度来看——组合是指从 n 个元素中选出 k 个元素的方式数(不考虑顺序)。其通用公式是:
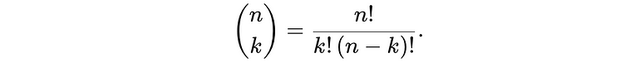
假设有 5 个对象,从中选出 3 个,那么我们可以选出多少种不同的组合?答案是:
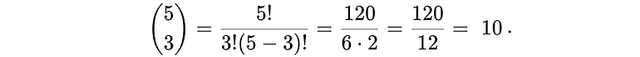
那我们从这 5 个对象中选出 0 个呢?
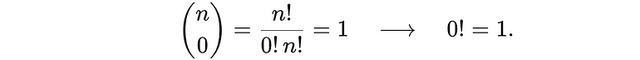
如果我们希望这个公式在 k = 0 的时候也成立,那我们就必须令 0! = 1。
这也符合我们的直觉:从一堆物品中不选任何一个,只有一种方式——什么也不选。
伽马函数
还有一种更抽象的解释,基于伽马函数(Gamma function)。这是一个将阶乘函数扩展到非正整数以外的连续函数,通常归功于瑞士博学家莱昂哈德·欧拉(Leonhard Euler)。
简单来说,伽马函数 Γ(z) 提供了一种方式,可以把阶乘函数推广到诸如 22/7 这样的非整数(甚至复数)。它通过一个积分定义:
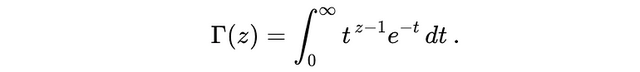
这是对正实数的定义。
它的一个关键性质是:
Γ(n + 1) = n!
因此:
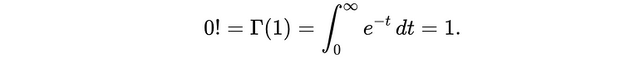
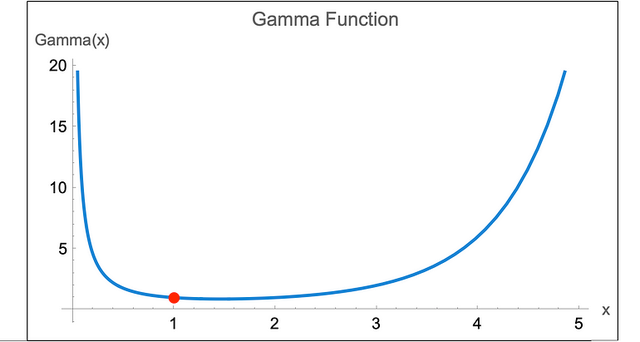
而图像显示,Γ(1) = 1,顺便说一下,标题图像是我们包含复数时 Gamma 函数行为的一种表示。
这就从一个完全不同的视角支持了同一个结论。
这篇文章并未穷尽所有解释。数学的奇妙之处之一,就在于它往往拥有多个视角,对同一问题呈现出万花筒般的不同面貌。
乍看之下,0! = 1 是一个不合情理的等式,然而深入思考你会发现,它既合乎逻辑,又出于必要,在不同语境下都有令人信服的理由。
这个小小的“1”,同时承载着代数的结构一致性、组合的抽象理解、积分理论的优雅定义和数学美的深邃奥义。
个人配资炒股配资提示:文章来自网络,不代表本站观点。



